Boggle
All code for this project is stored in this repository It contains:
- Boggle engine (also playable in console)
- Boggle GUI game
- Boggle solver (this is the interesting part)
Background and Motivation
Boggle is a word game, the objective is to collect words from a board of randomly distributed letters, here’s how it looks in my GUI:

The player picks a letter, then may pick any unpicked adjacent letter (diagonals included), untill they collect a word. Then they may check it against the game’s dictionary.
If the word appears in the dictonary, and hasn’t been found in this game, the player is awarded with points equaling the square of the length of the word.
The game continues untill the time runs out or all possible words (on this board) have been found.
I helped a student with a boggle game project, then I thought it would be neat to add a solver.
Boggle Game Implemetation Overview
View the code in the repository above for an in depth look, but here are some notes for the main elements:
BoggleEngine
This is the main game class, it stores the boggle grid and handles all game operations and actions, following boggle rules.
ImportBoggleDict
This function imports a dictionary of words (a txt file) and cleans it. Invalid words:
- Contain characters other than english letters.
- Contain a Q which isn’t followed by a U (otherwise the letter q becomes an obstacle in the game).
- Have less than 2 letters.
Any txt file of words seperated by line ends will work, I took USA ENGLISH - 66000 words from here.
GetLetterFrequenices
creates a 2 lists from the input dictionary - letters and their respective frequency of appearance in the dictionary.
This is used in the next function.
RandomBoard
Creates a 4x4 boggle board consisting of random (english) letters, sampled using the freuquency list as a probability distribution. This biased sampling makes generated boards likely to contain more words from the dictionary than just random sampling.
Imagine the dictionary only contained:
- road
- dad
- oar
- door
- odor
Let’s say we generate a boggle grid that doesn’t contain the letter O - we can only find the word ‘dad’! 4/5 words can’t be found on this grid, that’s a boring game.
Here is an example of a typical frequency distribution of letters in english.
PlayWithoutGUI
This runs the game loop, rendering and accepting input in the console.
Boggle GUI
This file runs a nice Matrix themed GUI for the game, using the engine in the background for all game operations. The GUI is divided to:
- MenuFrame - Where the player chooses to start a new game or quit.
- GameFrame - Where the boggling happens.
Solver
Broadly, the solver uses backtracking recursion to go to each cell in the boggle grid and find all words starting with that letter. However, just going to every adjacent cell and checking for words is very inefficient. There are two main inefficiencies -
- We must compare each collected word to the entire dictioary
- We go through a huge number of steps, even in a 4x4 grid, to cover all possible letter combinations, something of the order of magnitude of 7^16.
Here’s the trick:
- A new alphabet is created - a set containing only the letters which appear on the board.
- A new sub-dictionary is created which only contains words made only out of the letters in the new alphabet.
- Bonus: A set of words is created which contains all the words in the new dictionary AND all of their prefixes, e.g: PEANUT also adds PE,PEA,PEAN,PEANU
- When going through the recursive search, if the current collected word isn’t found in the set of prefixes - stop the recursion and backtrack.
We still compare each collected word to the set of words (the reduced set) to find if the current combination is a valid word.
In a 4x4 grid the maximal search depth (word length) is 16. However, longer words have less chance (significantly) to be prefixes to other words , therefore most combinations quickly reach a dead end.
For example, for our dictionary, the prefix distribution (vs letter count) is shown in the figure:
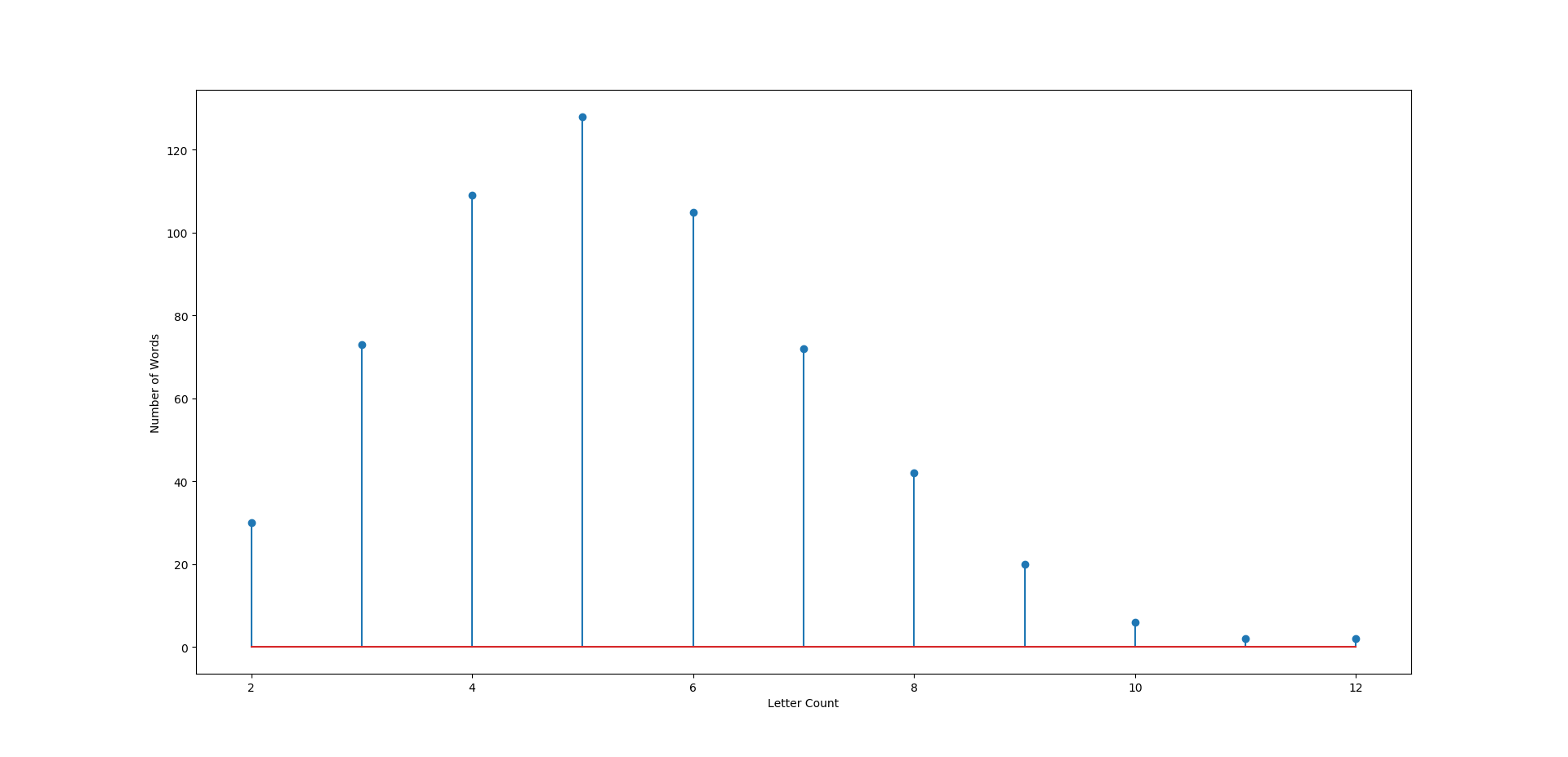
This algorithm typically finds all words on a boggle board in less than a second.
This solver is used to display the remaining words on the board in the GUI.