Klotski Solver
All code for this project is stored in this repository it contains:
- Klotski puzzle class definition
- A backtracking recursion solver
- Breadth first search solver
Background and Motivation
Klotski puzzle is a well known logic puzzle, here’s what’s called a default starting layout:
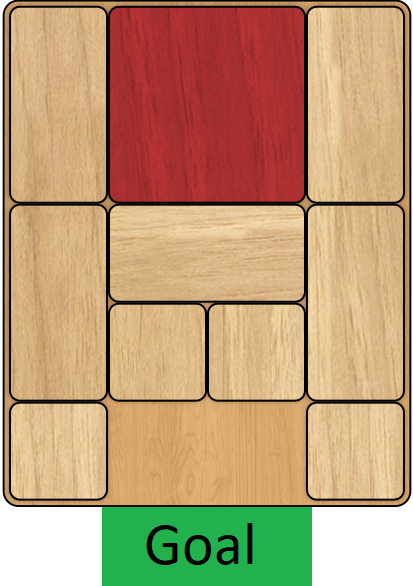 The objective is to move the blocks one at a time to a free space, untill the red block reaches the goal. A solution is the discrete set of moves to reach the victory conditions. The quality of a solution can be measured by the required number of moves.
The objective is to move the blocks one at a time to a free space, untill the red block reaches the goal. A solution is the discrete set of moves to reach the victory conditions. The quality of a solution can be measured by the required number of moves.
The optimal solution has been published in 1964 by Martin Gardner, in the February 1964 issue of Scientific American.
Note: There are different ways to count moves - in this post, any single movement of any single block is counted as a “move”.
I watched this video and I wanted to complete the challange - using backtracking recursion to solve the Klotski Puzzle (not necessarily getting the optimal solution). After solving this problem with recursion, I found a much cooler approach which is guaranteed to find the optimal solution - Breadth First Search. I will present both approaches in this post.
Puzzle Implemetation Overview
These objects are used to represent the game state in both solutions. There are two main object classes :
Blocks
There are the game blocks which populate the puzzle grid. These store:
- a number (ID).
- the cells occupied by the block.
- whether this is the target block (the red block in the picture) Blocks also own a move function, which shifts the occupied cells in a certain direction.
Klotski Puzzle
This is the main puzzle object, it contains all the blocks and tracks the state of the puzzle grid. This object also checks for the winning condition (red block reaches the goal).
Backtracking Recursion
Broadly, these are the function steps:
- Makes a list of all available moves from current state.
- Goes to the next available move state, and checks if:
- A state can be considered a dead end.
- A state statisfies the winning condition.
- Depending on whether the conditions are satisfied or not:
- No condiition satisfied - call self using the new state (go back to 1).
- 1st condition satisfied - backtrack (cancel the last move) untill niether condition is satisfied.
- 2nd condition satisfied - backtrack, exit the parent function and collect the path ([block,move]) - repeat untill you exit the recursion.
Note: A dead end is a state which doesn’t statisfy the winning condition and there are no available moves which reach a new state (previously unvisited). We save a list of all visited states in the form of hashed grid objects (see appendix) and check current grid state against all visited states at every call.
Note: This is essentially a depth first search
This algorithm only finds one, non optimal path (700+ moves). It theoretically could find other paths if the recursion wasn’t stopped when reaching the winning condition. However, on my machine I had to increase the recursion depth to 5000 and seem to reach stack overflow above that.
Breadth First Search
We view the puzzle as a (undirected) graph in the sense that each state is a node and neighboring nodes are states which can be reached with exactly one move.
Breadth first search (BFS) is a common technique for finding the shortes path in a graph. In our case, this finds the shortest path from the intial state to the victory state, and optionally several other unique paths.
In short, the BFS algorithm:
- Create a queue, put the intial node (state) as a node in the queue
- Create a set of visited states (hashed grids, see appendix)
- while the queue is not empty:
- Pop the first member in the queue
- Find all neighboring nodes to the state
- For each neighbor, if it wasn’t previously visited (check against the visited set):
a. Add the node ID (hashed grid) to the visited set.
b. Add the node to the end of the queue.
c. Remember the origin node as the parent of this neighbor node. d. If the node is the destination (satisfies winning condition), follow the node parents and create a path from this node to the intial state.
This algorithm keeps searching untill all nodes which are connected to the intial node (can be reached with legal moves) are visited. The function will return a list of unique paths, including the shortest path, in a matter of seconds.
The result is a path of 117 states (including the initial state). Since there are different ways to count moves, other answers give a different number for the same path. However this work seems to count moves in the same way, reaching the same optimal path.
Note: Python finds if a states is in a set MUCH quicker than in a list.
Appendix: Hashed Grids
Since finding a state in a list of visited state is critical to both algorithms, and used in each call/iteration, it’s important for this part to be as efficient as possible.
The grid is stored in the KP object as a list of lists - which block occupies each cell.
Storing and searching for a whole grid is pretty inefficient.
The hashing process translates a grid state to a unique string:
def GridHashKey(grid):
value_map = {0: ' ', 1: 'v', 2: 'v', 3: 's', 4: 'v', 5: 'v',
6: 's', 7: 'h', 8: 's',9:'s',10:'t',-2:'e', -1: 'w'}
chars = [value_map[s] for r in grid for s in r ]
hashed = ''.join(chars)
return hashedBoth approaches in this post collect sets of visited hashed strings and compare any current state (in hashed form) to the set of strings, this is relatively quick.