Huffman Coding

All code for this project is stored in https://github.com/ArikVoronov/HuffmanCoding

Background and Motivation

Huffman Coding is a compression algorithm, which allocates the encoding length of characters based on the frequency of their appearance.

Naive Encoding

Any character in a text is stored in memory as bits - sequences of 0s and 1s. Let’s say we don’t know anything about the text, so we need a generic way to encode each character which is unique and short as possible. There are several common standards for encoding characters, let’s take ASCII as an example.

ASCII attaches a running index number to each character. The character’s encoding is the binary representation of the index number.

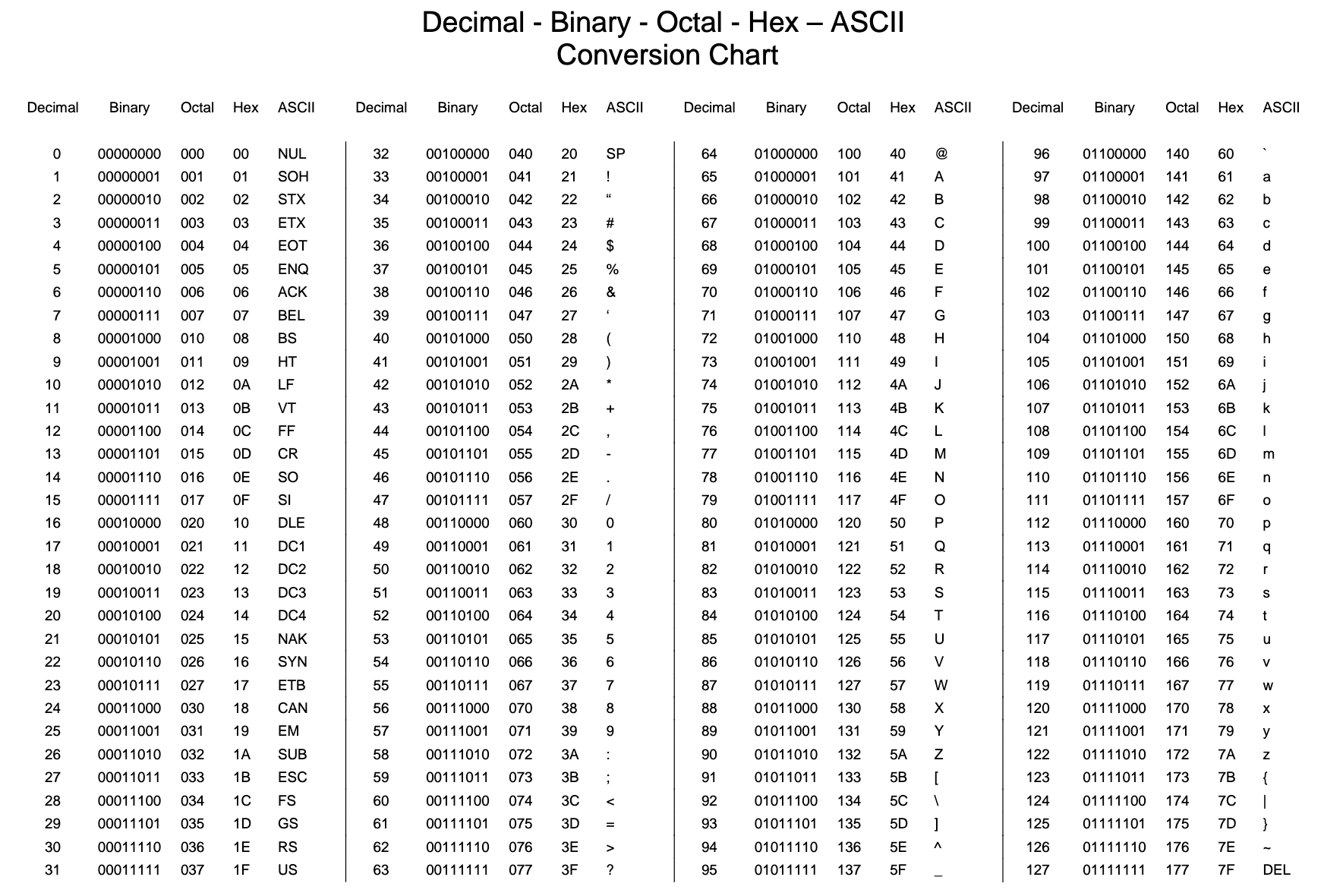
• Here is an interactive translation table.
• Here is a discussion about some pros and cons of the ASCII encoding.

In terms of compression, this is not ideal:
Every character requires exactly 7 bits of information. So, a character like “&”, which is rare in a literary text, gets the same amount of bits as “e” which is common.
A text consisting of N characters will take up a space of 7*N bits in storage.

Simple example for frequency based encoding

Let’s say we have the phrase “freeze geezer” and we want to encode it in bits.

Just for the sake of the example, let’s make our own naive and frequency based encodings.
Here’s a naive 3 bit encoding:

Character	Binary Encoding
f	000
r	001
e	010
z	011
	100
g	101

*The empty cell is a space character (between the two words).

Note: In this example, we need at least 3 bits for each character to have a unique binary encoding.

“freeze geezer” becomes:

000 001 010 010 011 010 100 101 010 010 011 010 001

This takes up (6+1+6)*3 = 39 bits of information.

Now, let’s make a simple frequency based encoding:

Character	Binary Encoding
f	1010
r	110
e	0
z	111
	1011
g	100

This is still a unique encoding, don’t worry about how exactly I got it just yet.

Note: The length of bits allocated to any character is based on the frequency with which it appears in our phrase:
- 'e' appears 6 times -> encoded to a short sequence - 0.
- 'f' appears only once- > encoded to a long sequence - 1010 (longer than the naive encoding!).

“freeze geezer” becomes

1010 110 0 0 111 0 1011 100 0 0 111 0 110

But this way only takes up only 29 bits of information! This is an imporvement of (1-29/35)*100=17%. Generaly, the compression will improve with longer phrases (up to a point), and at worst will be as good as a naive encoding.

Huffman Coding Algorithm Theory

To generalize the approach presented above, we need a systematic algorithm to derive our frequency based encoding. To make this as explicit as possible, I’m going to explain the algorithm steps with text compression in mind, but the method can be generalized to any file type. Also, to make this explanation a bit simpler, I’ll refer to character frequency as the number of times a character appears in the text.

Frequency count

We need to know the frequency of characters in the text, the simplest way is to go through the text one character at a time and count the number of appearances of each one.

Coding Tree

After we have the frequency count, we construct a tree data structure, which organizes the characters by their frequency.
Each node of the tree contains the cumulative frequency of all its children nodes.
In addition, every leaf (the bottom most node of any branch, without children) contains a character.

We organize the tree by pairing the nodes with the lowest frequency (n1, n2) and giving them a joint parent node (n3) which contains as a value the sum of frequencies (n3.frequency = n1.frequency + n2.frequency). For the sake of consistency, we keep the node with the larger frequency as the right child (could also be the other way, the important thing is to keep a consistent rule).

Here is the Huffman tree for the “freeze geezer” example:

Some observations:

1. Immediately on the right of the root node is a leaf with the ‘e’ char - which is the most frequent character.
2. The deepest nodes contain the characters ‘f’ and ‘ ‘(space) which are the least frequent
3. The root node contains the total cumulative frequency which is simply the amount of characters in the text - 13 in this case.

In the resulting structure the depth of each leaf is proportional to its frequency.

Encoding Dictionary

Travel the path from the root to a character, starting with an empty encoding:

• Going down the right branch we add a ‘0’ to the encoding
• Going down the left branch we add a ‘1’ to the encoding

For example, to get to the ‘f’ character from the root we travel:

left(1) -> right(0) -> left(1) -> right(0)

Checking the encoding table in the example above , the encoding for ‘f’ is exactly ‘1010’ !

Note:
1. Every character appears only once in the tree.
2. There's a unique path to any character from the root.
3. The length of the encoding is based on the depth of the character leaf.
Therefore, we get a unique frequency based encoding for each character!

Code Implementation

Here is the Python code implementing the steps described in the theory section

Pay attention to the comments in the code.

Frequency Count

def GetFrequency(data):
    '''
    This function takes a text data string and creates a frequency dictionary
    of the form 
    Input: character string
    Output: a dictionary of the form {character:frequency}
    '''
    freqDict = {}
    for c in data:
        if c not in freqDict:
            freqDict[c] = 1
        else:
            freqDict[c]+=1
    return freqDict

Coding Tree

Node class, along with a function which connects 2 children to a parent node

class Node():
    '''
    The Huffman Tree consists of these nodes, which contain both the frequency 
    and a character (if available)
    '''
    def __init__(self,value=None,char=None):
        self.value = value
        self.char = char
        self.parent = None
        self.children = [None, None]
    def Connect2(self,n1,n2):
        '''
        This function connects two children nodes n1,n2 to the current node.
        For consistency with other functions, n2.value must be greater or equal than n1.value
        '''
        assert(n2.value>=n1.value)
        self.value = n1.value+n2.value
        n1.parent ,n2.parent= self, self
        self.children = [n1,n2]

Helper sorting function

def SortDictionary(dictionary):
    '''Sort a dictionary by values'''
    return {k: v for k, v in sorted(dictionary.items(), key=lambda item: item[1])}

Create a Huffman Coding Tree

def HuffmanCodingTree(freqDict):
    '''
    This function builds a Huffman Coding tree of Nodes
    Input: dictionary of the form {character:frequency}
    Output: root node of the tree
    '''
    leafNodesList=[] # This list stores leaf nodes, which contain characters
    internalNodesList=[] # This list stores internal nodes, which serve as parents to other nodes
    sortedDictionary = SortDictionary(freqDict) # The dictionary must be sorted (lower values first)
    for k,v in sortedDictionary.items():
        leafNodesList.append(Node(v,k))
    while True:
        if not leafNodesList and len(internalNodesList)==1:
            # When only one last node is left in the internal nodes array,
            # that is the root of the tree
            root = internalNodesList[0]
            return root
        # Create a list of candidates for lowest values - 2 at most from each list (internal/leaf)
        # A 'candidate' stores a node and its respective list
        candidates = []
        for i in internalNodesList[:2]:
            candidates.append([i,internalNodesList])
        for j in leafNodesList[:2]:
            candidates.append([j,leafNodesList])
        candidates.sort(key= lambda x: x[0].value) # Sort the candidates by value - lowest first
        # Keep the 2 candidates with the lowest values, then pop them out of their respective lists
        n1 = candidates[0][0]
        candidates[0][1].pop(0)
        n2 = candidates[1][0]
        candidates[1][1].pop(0)
        # Create a parent node (internal) to the candidates and put it last in the internal list
        # This keeps the internal list also sorted (ascending) 
        # since the 2 child values summed are larger at every iteration 
        newNode = Node()
        newNode.Connect2(n1,n2)
        internalNodesList.append(newNode)

Encoding Dictionary

def MakeCodesDict(node,code,codesDict):
    '''
    This regression function creates a Huffman encoding dictionary out of a tree
    Input:
        node - current node in tree (initially the root)
        code - encoding up to current place in tree
        codesDict - Huffman encoding dictionary (initially an empty dictionary)
    
    '''
    if node.children == [None,None]:
        codesDict[node.char]=code
    else:
        MakeCodesDict(node.children[0],code+'0',codesDict) # traveling to the smaller value add 0
        MakeCodesDict(node.children[1],code+'1',codesDict) # traveling to the larger value add 1

Encoding and Decoding Text

Finally, we use the coding dictionary and tree to encode/decode any given text

def EncodeText(text,codesDict):
    '''
    This function encodes a given text, using the provided encoding dictionary
    Input:
        text: a string
        codesDict: (Huffman) encoding dictionary
    Output: encoded text, a string of '1's and '0's
    '''
    encoded = ''
    for c in text:
        encoded+=codesDict[c]
    return encoded

def DecodeText(text,hctRoot):
    '''
    This function decodes a Huffman encoded text, using the respective Huffman tree
    Input:
        text: a string of '1's and '0' encoded with a dictionary created from the provided tree
        hct: Huffman Coding Tree root node
    Output: decoded text string
    '''
    decoded = ''
    currentNode = hctRoot
    for n in text:
        currentNode = currentNode.children[int(n)]
        if currentNode.children ==[None,None]:
            decoded+=currentNode.char
            currentNode = hctRoot
    return decoded

Implementing the Code

Let’s try some compression on a real text. You can download some free books from Project Gutenberg. I picked “Heart of Darkness” by Joseph Conrad.

First of all, read the text and convert it to a binary (ascii) encoding

with open("heart_of_darkness.txt", "rb") as f:
    text = f.read()
text = text.decode()
textPartial = text[:15000]
binText = bin(reduce(lambda x, y: 256\*x+y, (ord(c) for c in textPartial), 0))

This is a pretty long text, to save some computing time I took only a part of it for comparison (first 15000 chars).

Next, go through the steps described above to get the Huffman tree and encoded text

freqDict = GetFrequency(textPartial)
hctRoot = HuffmanCodingTree(freqDict)
codesDict = {}
MakeCodesDict(hctRoot,'',codesDict)
huffmanText = EncodeText(textPartial,codesDict)

We can also check that the result is decodable back to the original text:

decoded = DecodeText(huffmanText,hctRoot)

Last, check the compression percentage using the formula:

compression = ( 1-(len(huffmanText)/len(binText)) )*100

We can run these steps for a different amount of characters, to see the effect of the length of the text on the compression rate.
here is the resulting plot for char count from 1000 to 15000

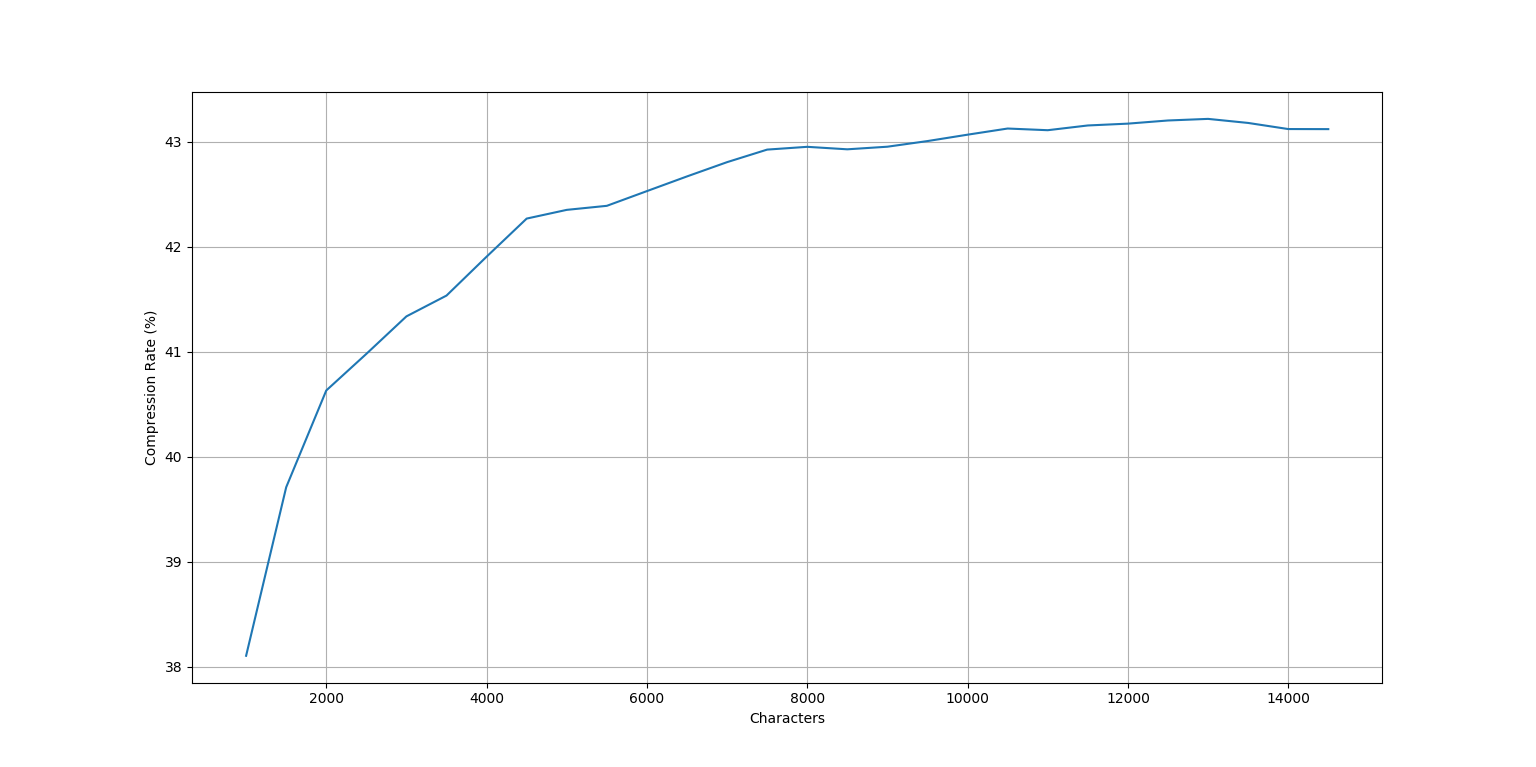
The compression somewhat improves with the length of the text, and seems to be asymptotic, reaching a limit value of about 43% at ~8000 chars.